Esta publicación está inspirada en la presentación de Kaushik Punjabi a London Value Investing Club. Sin embargo, el contenido de la publicación es la opinión del autor.
Siempre escuchamos que deberíamos empezar a ahorrar para la jubilación antes de tiempo. Deberíamos reinvertir nuestro dividendos y encuentre productos que ofrezcan composición. Una tasa de interés ligeramente más alta puede traducirse en un valor final mucho más alto. ¿Qué tan ciertos son estos? ¿Qué tan poderoso es el interés compuesto? Depende de los tres factores de 1) tiempo, 2) tasa de interés y 3) inversión recurrente.
Los tres factores
1 vez
El primer factor es el tiempo. La fórmula de interés compuesto simple, sin inversiones adicionales, es
Cantidad t = P (1 + r⁄norte )Nuevo Testamento
Dónde
- P es el monto principal (inversión inicial),
- r es la tasa de interés nominal anual,
- n es el número de veces que se capitaliza el interés por año,
- t es el número de períodos de capitalización.
En su forma fundamental, esta es una función de potencia y = c X (algún número constante elevado a un exponente variable y un principal de “1”). Si miramos esta gráfica de la función de potencia fundamental, podemos ver el cambio en y cuando x aumenta. Si usa la fórmula y = c X donde c es 3 y x sigue aumentando de 1 a 5, puede ver que y aumenta de 3 a 243.
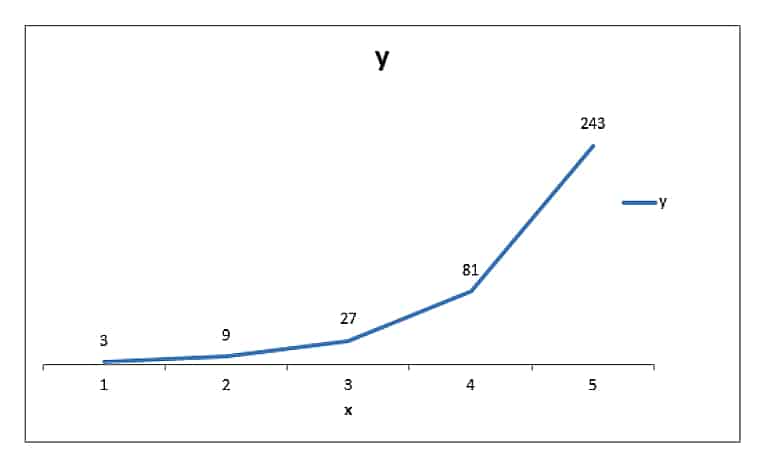
En finanzas, tenemos constantes mucho más pequeñas que tres (tres serían un rendimiento de 300% por período), pero la idea se mantiene. Cuanto más tiempo se aplica una tasa de interés a una inversión, más "poderoso" se vuelve el interés. También debe tenerse en cuenta que la salida del gráfico se aplica a un principal de 1 (USD, GBP, EUR, lo que sea). Tenemos directores mucho más grandes y plazos más largos en finanzas.
Un ejemplo más realista en finanzas:
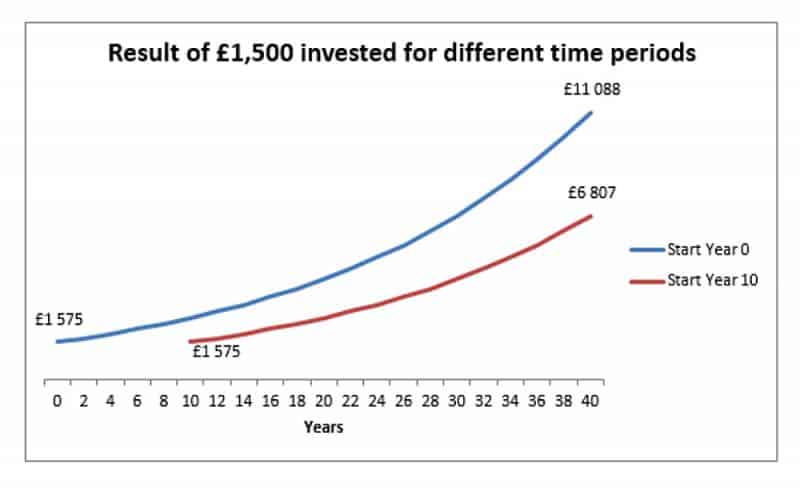
El siguiente cuadro representa una inversión única de £ 1,500 con una tasa de interés constante de 5%. El primero comenzó a invertir al comienzo del año 0 y el segundo al comienzo del año 10 (es decir, 10 años después). Al momento de la jubilación (40 años compuestos para el año 0, 30 años compuestos para el año 10), la inversión anterior vale 63% más.
2. Tasa de interés
El segundo factor importante es la tasa de interés. A medida que crece la tasa de interés, también lo hace el rendimiento a lo largo del tiempo. En números exagerados, podemos ver que 33 (27) es mucho mayor que 23 (8) en comparación con los valores base iniciales de dos y tres.
Esta diferencia en las tasas (3-2 = 1 = 100%) rara vez ocurre en finanzas, pero el principio se mantiene en escalas menores. En escalas cortas (como los tres períodos de nuestro ejemplo), la diferencia tiende a ser pequeña. Pero en escalas de tiempo más largas, como 40 períodos (cuarenta años de inversión), podemos ver las diferencias: (1 + 5%)40 = 700% mientras que (1 + 8%)40 = 2100%.
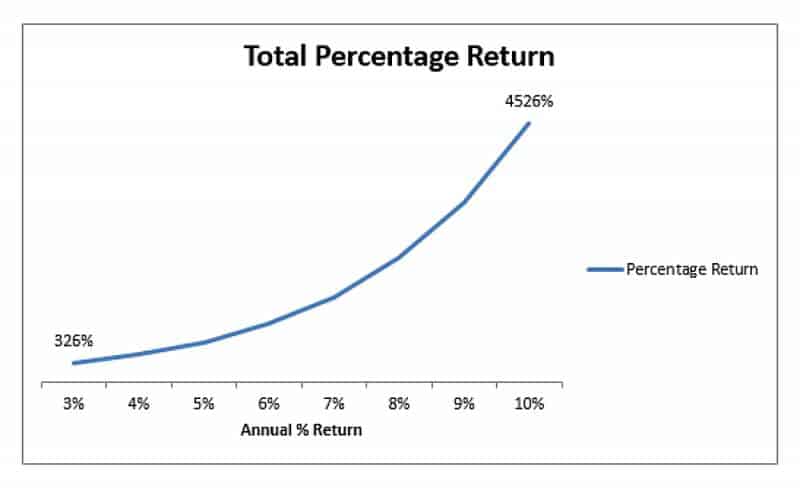
El cuadro a continuación muestra el rendimiento porcentual para un valor de inversión compuesto simple de depósito único durante cuarenta años. La única variable es la tasa de interés. Como podemos ver, el rendimiento crece exponencialmente, al igual que la forma en que el componente de tiempo afecta el rendimiento. Al cabo de cuarenta años, 3% nos devuelve 325% mientras que la tasa de 10% nos dio 4500%. Para un depósito inicial de £ 1,500, eso es £ 4,875 versus £ 67,500.
3. Inversiones recurrentes
En los ejemplos anteriores, hicimos depósitos simples y únicos y luego nos basamos completamente en el interés compuesto para generar retornos. Pero en la mayoría de los planes de inversión y ahorro, realizamos depósitos periódicos para aumentar nuestro capital.
No hay una función de forma cerrada para esto, por lo que tenemos que usar una función recursiva. Si asumimos que el depósito se realiza a principios de año, para que el interés se aplique al depósito, obtenemos lo siguiente:
Cantidad este periodo = (Cantidad Último periodo + depósito) × (1 + tasa de interés)
Debemos recalcular para cada período, como Cantidad Último periodo cambios para cada período. Cuando realiza depósitos, no solo aumenta el capital base (la cantidad de inversión pura) sino que también aumenta la cantidad que gana intereses.
Por eso es importante comenzar temprano. Si deposita £ 500 al comienzo de cada año y comienza en el año 10, se perderá un pago de interés para el depósito del año 9, dos años de interés para el depósito del año 8, y así sucesivamente. Su depósito inicial aumentaría en £ 5,000, pero también ganaría intereses de alrededor de £ 1,300 solo sobre los depósitos durante los 10 años.
Este gráfico muestra el valor final de una inversión de 40 años de 5% con un depósito inicial de £ 1,500 y cantidades variables de depósitos anuales.
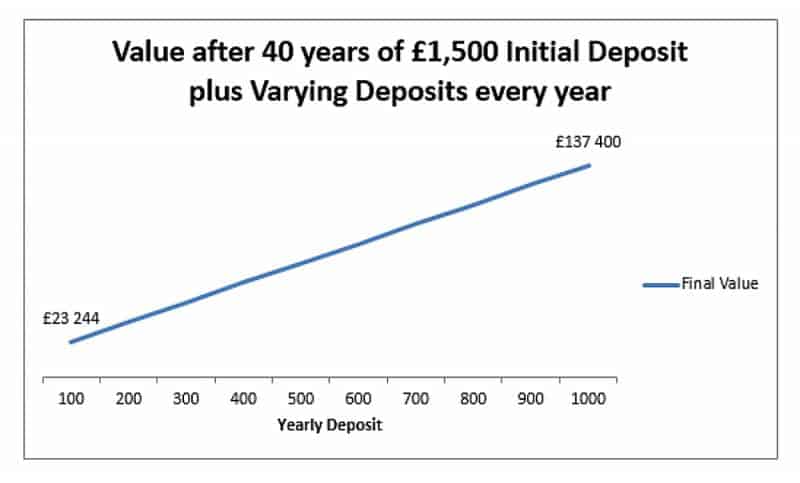
Podemos ver que los cambios en el depósito anual son menos importantes que los cambios en el interés o el tiempo, ya que tenemos una relación lineal en lugar de exponencial. Pero en números absolutos, el depósito sigue siendo importante. £ 140,000 es mucho mayor que £ 20,000. Al depositar £ 100 40 veces, terminamos con una inversión adicional de £ 4000, por lo que tenemos alrededor de £ 17,500 en intereses devengados. Con 1000 libras esterlinas depositadas cada año, depositar 40.000 libras esterlinas adicionales, pero nuestro interés total devengado es mucho mayor, 96.000 libras esterlinas.
Ganamos más interés sobre el mayor interés producido por los depósitos más altos. ¿La comida para llevar? Más interés genera más interés (y esta es la razón del dicho “los ricos se hacen más ricos”).
¿Qué pasa si no reinvertimos nuestros dividendos o intereses?
Quizás simplemente queremos acumular nuestros pagos de intereses, pero no los reinvertimos. Si hacemos esto, no ganaremos intereses por ellos. Eso significa que tenemos interés no compuesto. ¿Cómo se compara?
Este gráfico muestra una inversión inicial de £ 1,500 sin otros depósitos (por lo que ignoramos por completo los pagos recurrentes). Tenemos dos variables: una es la tasa de interés (5% frente a 6%) y la otra es capitalización o no (CIE = interés compuesto ganado, NCIE = interés no compuesto ganado).
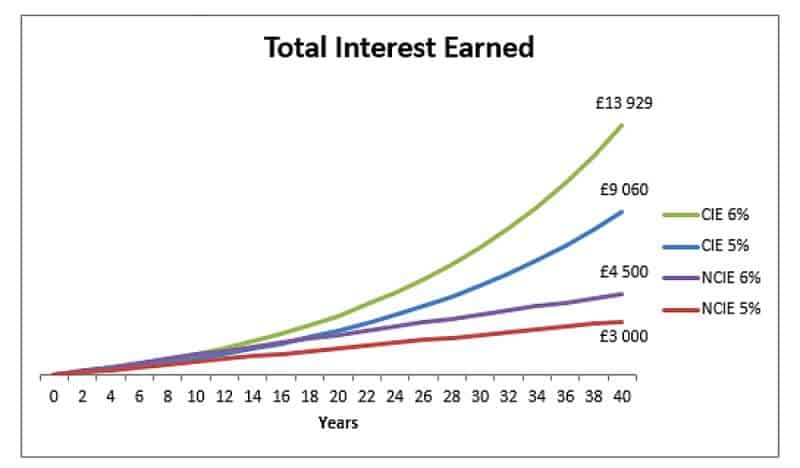
Las líneas NCIE son lineales porque simplemente multiplicamos el número de períodos por el interés que generamos cada año. Ganamos £ 75 de interés sobre el depósito de £ 1,500 (para 5%), y eso nunca cambia. Lo acumulamos lentamente, £ 75 a la vez. Pero con la capitalización, podemos ver que el primer año es de £ 75, pero el próximo año ganamos £ 78.75 [(1500 + 75) × 1.05 - 1575], un extra de £ 3.75, que a su vez contribuye a la acumulación futura de intereses. Esto sigue creciendo con el tiempo.
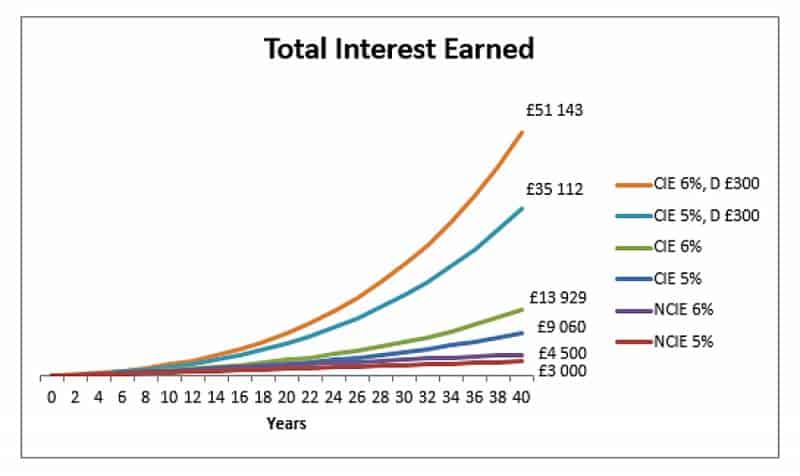
Aquí está el mismo gráfico con capitalización para 5% y 6% pero con depósitos anuales de £ 300:
Y un último gráfico, que muestra lo que sucedería si comenzáramos un plan de inversión con depósitos de £ 250 a 5%, pero lo comenzamos 10 años después.
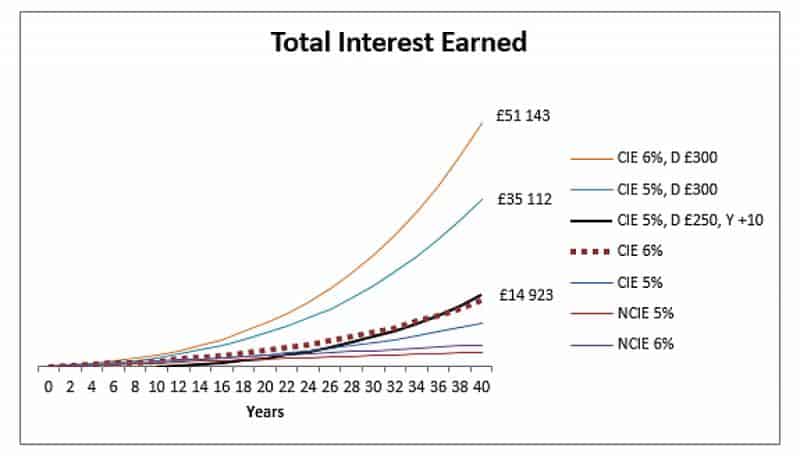
Lo más importante a tener en cuenta aquí es que, debido a que la inversión se inicia 10 años después y la tasa de interés es más baja, el inversor debe depositar £ 250 cada año solo para igualar la línea 6% sin depósito. Durante el período de 30 años, eso es un desembolso adicional de £ 7,500 solo debido a un inicio tardío y una tasa de interés que es 1% más baja.
Además, también deberíamos considerar que 40 años de depósitos de £ 300 agregarán £ 12,000 de capital, además de la inversión original y los intereses devengados.
Resumen
Los dos componentes principales del interés compuesto (tiempo y tasa de interés) junto con los depósitos recurrentes pueden marcar una gran diferencia en cuánto crece su inversión con el tiempo. La rentabilidad de la renta variable entre 2004 y 2017 fue de 7,7% (Fuente: Schroders). Eso significa una divergencia aún más dramática entre los planes no compuestos y compuestos. Y como podemos ver, si está dejando dinero para la jubilación tardía, sus hijos o incluso sus nietos, el interés compuesto solo se vuelve más poderoso con el tiempo.
Un punto importante a tener en cuenta es que su interés compuesto debe estar por encima de la inflación. Mantener los activos en cuentas con intereses muy bajos no cubrirá la inflación, lo que significa que la cantidad bruta de dinero crecerá pero su poder adquisitivo permanecerá estancado (o, en el peor de los casos, incluso disminuirá).
En CityFALCON, ayudamos a los principiantes en finanzas a ser inteligentes e independientes al tomar sus decisiones financieras. Si está interesado en los mercados de valores, puede probar nuestro asistente de introducción aquí.




23/07/2018 a las 7:52 pm
bastante informativo y bien explicado
27/07/2018 a las 9:03 am
¡Buena publicación de blog!