Cet article est inspiré de la présentation de Kaushik Punjabi à Club d'investissement de valeur de Londres. Le contenu du message est cependant l'avis de l'auteur.
Nous entendons toujours dire que nous devrions commencer à épargner tôt pour la retraite. Nous devrions réinvestir notre dividendes et trouvez des produits qui offrent une composition. Un taux d'intérêt légèrement plus élevé peut se traduire par une valeur finale beaucoup plus élevée. Est-ce vrai? Quelle est la puissance de l'intérêt composé? Cela dépend des trois facteurs suivants: 1) temps, 2) taux d'intérêt et 3) investissement récurrent.
Les trois facteurs
Une fois
Le premier facteur est le temps. La formule simple des intérêts composés, sans autres investissements, est
Montant t = P (1 + r⁄n )NT
Où
- P est le montant principal (investissement initial),
- r est le taux d'intérêt nominal annuel,
- n est le nombre de fois où l'intérêt est composé par an,
- t est le nombre de périodes de composition.
Dans sa forme fondamentale, il s'agit d'une fonction puissance y = c X (un certain nombre constant élevé à un exposant variable et un principal de «1»). Si nous regardons ce graphique de la fonction de puissance fondamentale, nous pouvons voir le changement de y lorsque x augmente. Si vous utilisez la formule y = c X où c est 3, et x continue d'augmenter de 1 à 5, vous pouvez voir que y augmente de 3 à 243.
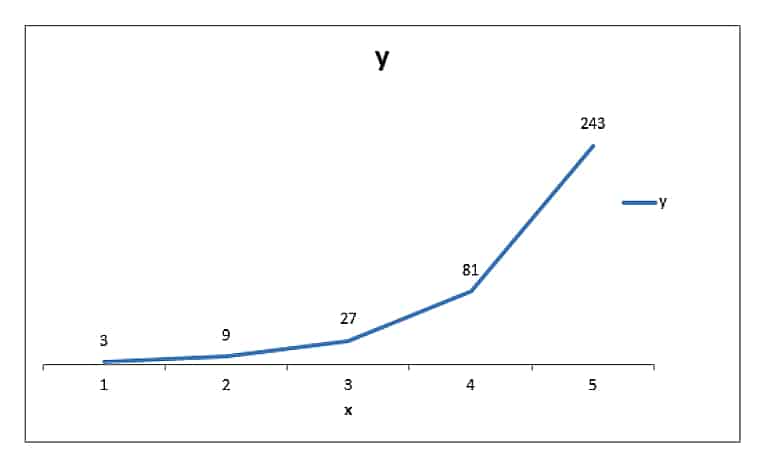
En finance, nous avons des constantes beaucoup plus petites que trois (trois seraient un rendement de 300% par période), mais l'idée tient. Plus un taux d'intérêt est appliqué à un investissement, plus l'intérêt devient «puissant». Il convient également de noter que la sortie du graphique est appliquée à un principal de 1 (USD, GBP, EUR, peu importe). Nous avons des mandants beaucoup plus importants et des délais plus longs dans le domaine des finances.
Un exemple plus réaliste en finance:
Le graphique ci-dessous représente un investissement ponctuel de 1500 £ avec un taux d'intérêt constant de 5%. Le premier a commencé à investir au début de l'année 0 et le second au début de l'année 10 (soit 10 ans plus tard). Au moment de la retraite (40 ans composés pour l'année 0, 30 ans composés pour l'année 10), l'investissement antérieur vaut 63% de plus.
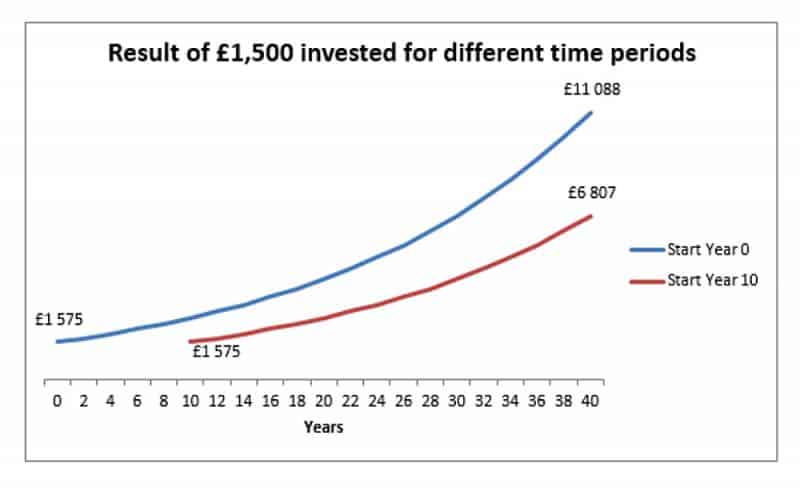
2. Taux d'intérêt
Le deuxième facteur important est le taux d'intérêt. À mesure que le taux d'intérêt augmente, le rendement augmente avec le temps. En nombres exagérés, nous pouvons voir que 33 (27) est beaucoup plus grand que 23 (8) par rapport aux valeurs de base initiales de deux et trois.
Cette différence de taux (3-2 = 1 = 100%) se produit rarement en finance, mais le principe est valable à des échelles plus petites. Sur des échelles courtes (comme les trois périodes de notre exemple), la différence a tendance à être faible. Mais sur des échelles de temps plus longues, comme 40 périodes (quarante ans d'investissement), on peut voir les différences: (1 + 5%)40 = 700% tandis que (1 + 8%)40 = 2100%.
Le graphique ci-dessous montre le rendement en pourcentage pour une valeur de placement composée à un dépôt unique sur une période de quarante ans. La seule variable est le taux d'intérêt. Comme nous pouvons le voir, le retour augmente de façon exponentielle, tout comme la façon dont la composante temporelle affecte le retour. Au bout de quarante ans, 3% nous renvoie 325% tandis que le taux 10% nous donne 4500%. Pour un dépôt initial de 1500 £, cela représente 4875 £ contre 67500 £.
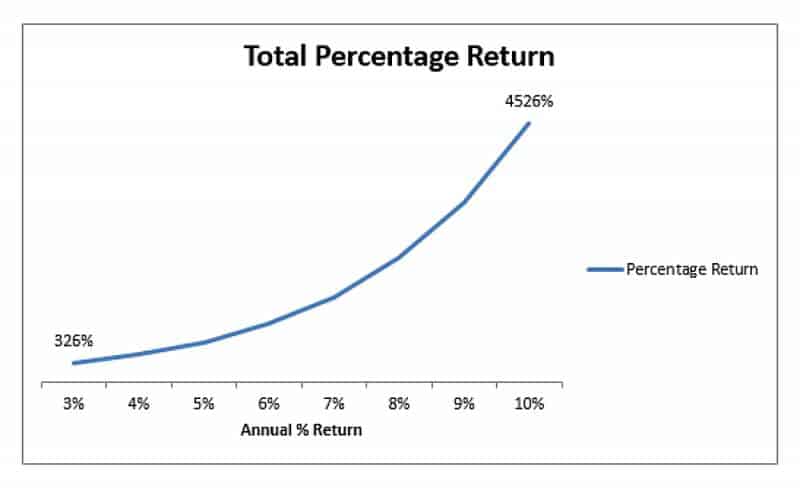
3. Investissements récurrents
Dans les exemples ci-dessus, nous avons fait des dépôts simples et uniques, puis nous nous sommes fondés entièrement sur des intérêts composés pour générer des rendements. Mais dans la plupart des plans d'investissement et d'épargne, nous faisons des dépôts périodiques pour augmenter notre capital.
Il n'y a pas de fonction de forme fermée pour cela, nous devons donc utiliser une fonction récursive. Si nous supposons que le dépôt est effectué au début de l'année, de sorte que les intérêts soient appliqués au dépôt, nous obtenons ce qui suit:
Montant cette période = (Montant la dernière Epoque + acompte) × (1 + taux d'intérêt)
Nous devons recalculer pour chaque période, comme Montant la dernière Epoque change pour chaque période. Lorsque vous effectuez des dépôts, vous augmentez non seulement le capital de base (le montant de l'investissement pur), mais vous augmentez également le montant qui rapporte des intérêts.
C'est pourquoi il est important de commencer tôt. Si vous déposez 500 £ au début de chaque année et que vous avez commencé la 10e année, vous manquerez un paiement d'intérêts pour le dépôt de l'année 9, deux ans d'intérêts pour le dépôt de l'année 8, et ainsi de suite. Votre dépôt initial augmenterait de 5 000 £, mais vous gagneriez également des intérêts d'environ 1 300 £ sur les seuls dépôts au cours des 10 années.
Ce graphique montre la valeur finale d'un investissement 5% sur 40 ans avec un dépôt initial de 1500 £ et des montants variables de dépôts annuels.
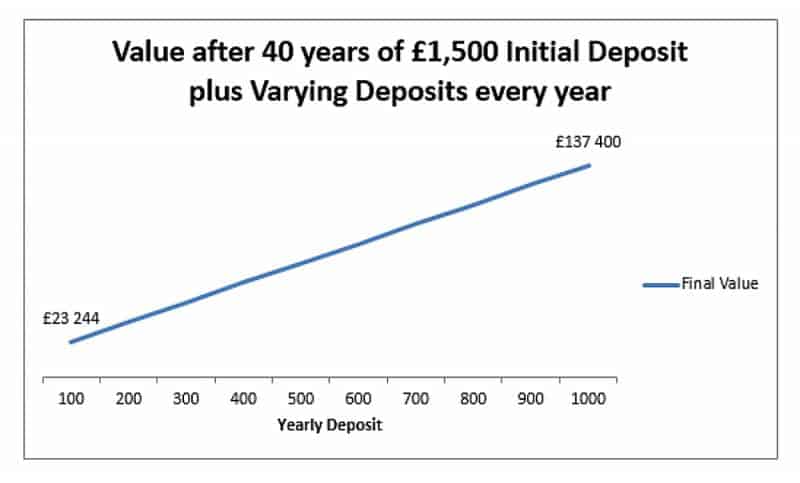
Nous pouvons voir que les changements dans le dépôt annuel sont moins importants que les changements d'intérêt ou de temps, car nous avons une relation linéaire au lieu d'une relation exponentielle. Mais en chiffres absolus, le gisement est toujours important. 140 000 £ est bien supérieur à 20 000 £. En déposant 100 £ 40 fois, nous nous retrouvons avec un investissement supplémentaire de 4000 £, nous avons donc environ 17500 £ d'intérêts gagnés. Avec 1000 £ déposés chaque année, nous dépôt un supplément de 40 000 £, mais notre intérêt total gagné est beaucoup plus élevé à 96 000 £.
Nous avons gagné plus d'intérêts sur les intérêts produits par les dépôts plus élevés. Les plats à emporter? Plus d'intérêt engendre plus d'intérêt (et c'est la raison du dicton «les riches deviennent plus riches»).
Et si nous ne réinvestissons pas nos dividendes ou nos intérêts?
Nous voulons peut-être simplement accumuler nos paiements d'intérêts, mais nous ne les réinvestissons pas. Si nous faisons cela, nous ne gagnerons pas d'intérêts sur eux. Cela signifie que nous avons un intérêt non composé. Comment cela se compare-t-il?
Ce graphique montre un investissement initial de 1500 £ sans autres dépôts (nous ignorons donc complètement les paiements récurrents). Nous avons deux variables: l'une est le taux d'intérêt (5% vs 6%), et l'autre est composé ou non (CIE = intérêts composés gagnés, NCIE = intérêts non composés gagnés).
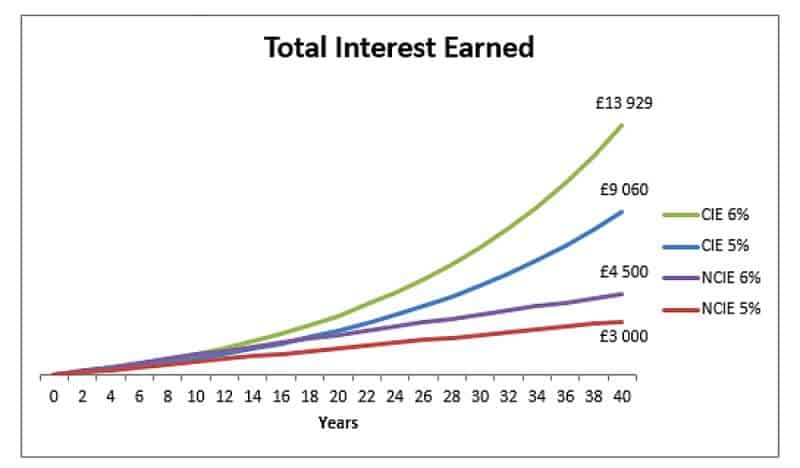
Les lignes NCIE sont linéaires car nous multiplions simplement le nombre de périodes par l'intérêt que nous générons chaque année. Nous faisons 75 £ d'intérêts sur le dépôt de 1500 £ (pour 5%), et cela ne change jamais. Nous l'accumulons lentement, 75 £ à la fois. Mais avec la composition, nous pouvons voir que la première année est de 75 £, mais l'année suivante, nous gagnons 78,75 £ [(1500 + 75) × 1,05 - 1575], un supplément de 3,75 £, qui contribue lui-même à l'accumulation future des intérêts. Cela continue de croître avec le temps.
Voici le même graphique avec la composition pour 5% et 6% mais avec des dépôts annuels de 300 £:
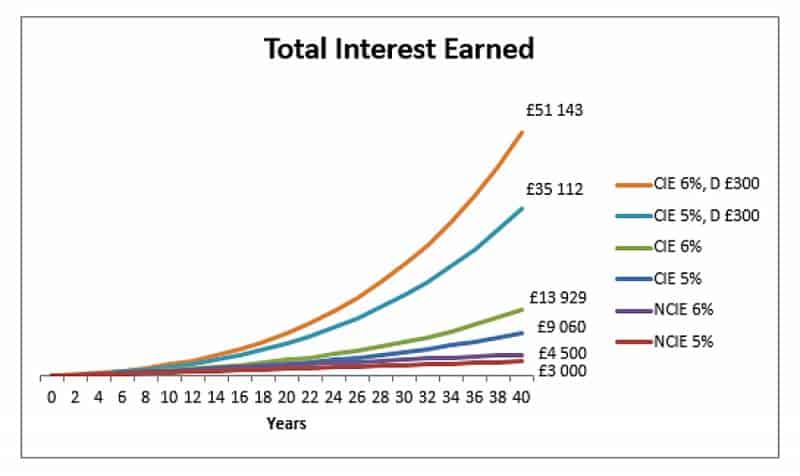
Et un dernier graphique, montrant ce qui se passerait si nous commençions un programme d'investissement avec des dépôts de 250 £ à 5%, mais nous l'avons commencé 10 ans plus tard.
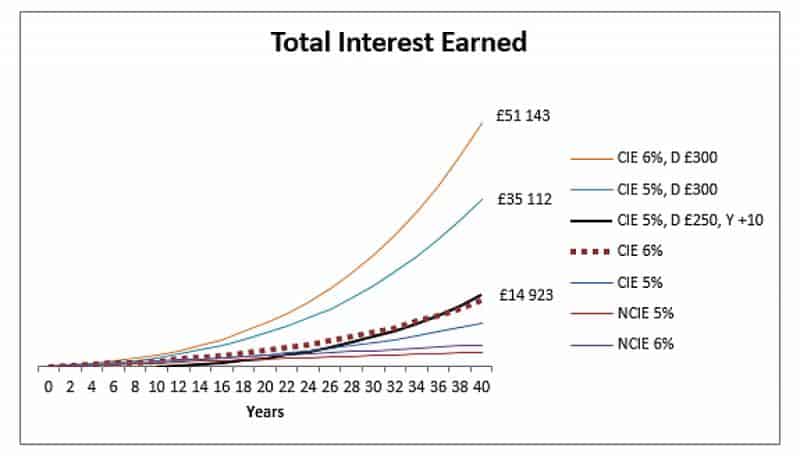
La chose la plus importante à noter ici est que, comme l'investissement est commencé 10 ans plus tard et que le taux d'intérêt est plus bas, l'investisseur doit déposer 250 £ chaque année juste pour correspondre à la ligne sans dépôt 6%. Sur la période de 30 ans, cela représente un supplément de 7500 £ juste à cause d'un démarrage tardif et d'un taux d'intérêt inférieur de 1%.
De plus, nous devons également considérer que 40 ans de dépôts de 300 £ ajouteront 12 000 £ en principal, en plus de l'investissement initial et des intérêts gagnés.
Sommaire
Les deux principaux éléments de l'intérêt composé (temps et taux d'intérêt) associés aux dépôts récurrents peuvent faire une énorme différence dans la croissance de votre investissement au fil du temps. Le rendement des actions entre 2004 et 2017 était de 7,7% (Source: Schroders). Cela signifie une divergence encore plus dramatique entre les plans non composés et composés. Et comme nous pouvons le voir, si vous laissez de l'argent pour une retraite tardive, vos enfants ou même vos petits-enfants, l'intérêt composé ne fait que devenir plus puissant avec le temps.
Un point important à noter est que votre intérêt composé doit être supérieur à l'inflation. La conservation des actifs dans des comptes à très faible taux d'intérêt ne couvrira pas l'inflation, ce qui signifie que la somme brute augmentera mais que son pouvoir d'achat restera stagnant (ou, dans le pire des cas, diminuera même).
Chez CityFALCON, nous aidons les débutants en finance à devenir avertis et indépendants dans la prise de leurs décisions financières. Si vous êtes intéressé par les marchés boursiers, vous pouvez essayer notre assistant de mise en route ici.




23/07/2018 à 19h52
assez informatif et bien expliqué
27/07/2018 à 9h03
Bel article de blog!