Questo post è ispirato alla presentazione di Kaushik Punjabi a Club di investimento di valore di Londra. Il contenuto del post è tuttavia il punto di vista dell'autore.
Sentiamo sempre che dovremmo iniziare a risparmiare per la pensione in anticipo. Dovremmo reinvestire il nostro dividendi e trova prodotti che offrono compounding. Un tasso di interesse leggermente più alto può tradursi in un valore finale molto più alto. Quanto sono vere? Quanto è potente l'interesse composto? Dipende dai tre fattori di 1) tempo, 2) tasso di interesse e 3) investimento ricorrente.
I tre fattori
1 volta
Il primo fattore è il tempo. La semplice formula dell'interesse composto, senza ulteriori investimenti, lo è
Quantità t = P ( 1 + r⁄n )nt
Dove
- P è l'importo principale (investimento iniziale),
- r è il tasso di interesse nominale annuo,
- n è il numero di volte in cui l'interesse viene composto ogni anno,
- t è il numero di periodi di composizione.
Nella sua forma fondamentale, questa è una funzione di potenza y = C X (un numero costante elevato a un esponente variabile e un principio di "1"). Se osserviamo questo grafico della funzione di potenza fondamentale, possiamo vedere la variazione di y all'aumentare di x. Se usi la formula y = c X dove c è 3, e x continua ad aumentare da 1 a 5, puoi vedere che y aumenta da 3 a 243.
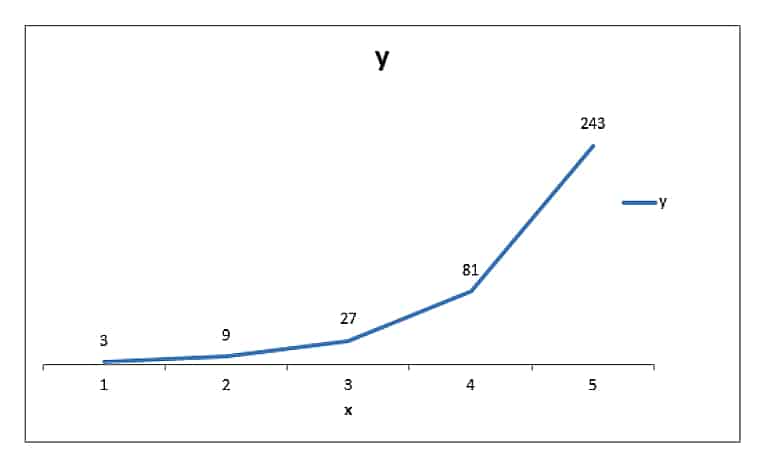
In finanza, abbiamo costanti molto più piccole di tre (tre sarebbe un rendimento di 300% per periodo), ma l'idea è valida. Più a lungo viene applicato un tasso di interesse a un investimento, più "potente" diventa l'interesse. Va inoltre notato che l'output per il grafico viene applicato a un capitale di 1 (USD, GBP, EUR, qualunque cosa). Abbiamo presidi molto più grandi e tempi più lunghi nella finanza.
Un esempio più realistico in finanza:
Il grafico sottostante rappresenta un investimento una tantum di £ 1.500 con un tasso di interesse costante di 5%. Il primo ha iniziato a investire all'inizio dell'anno 0 e il secondo all'inizio dell'anno 10 (ovvero 10 anni dopo). Al momento del pensionamento (40 anni composti per l'anno 0, 30 anni composti per l'anno 10), l'investimento precedente vale 63% in più.
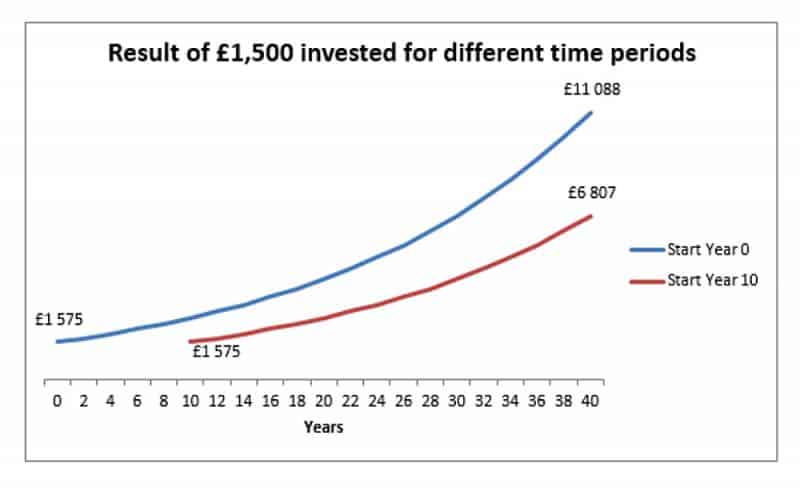
2. Tasso di interesse
Il secondo fattore importante è il tasso di interesse. Man mano che il tasso di interesse cresce, aumenta anche il rendimento nel tempo. In numeri esagerati, possiamo vedere che 33 (27) è molto più grande di 23 (8) rispetto ai valori di base iniziali di due e tre.
Questa differenza di tassi (3-2 = 1 = 100%) si verifica raramente in finanza, ma il principio vale su scale più piccole. Su scale brevi (come i tre periodi nel nostro esempio), la differenza tende ad essere piccola. Ma su scale temporali più lunghe, come 40 periodi (quaranta anni di investimento), possiamo vedere le differenze: (1+5%)40 = 700% mentre (1+8%)40 = 2100%.
Il grafico seguente mostra il rendimento percentuale per un semplice valore di investimento composto da un deposito una tantum nell'arco di quarant'anni. L'unica variabile è il tasso di interesse. Come possiamo vedere, il rendimento cresce in modo esponenziale, proprio come la componente temporale influisce sul rendimento. Alla fine dei quarant'anni, 3% ci restituisce 325% mentre il tasso 10% ci ha dato 4500%. Per un deposito iniziale di £ 1.500, sono £ 4.875 contro £ 67.500.
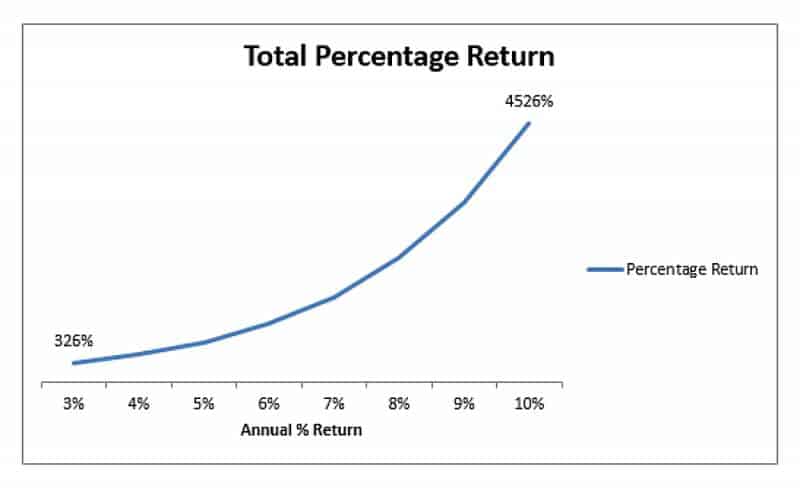
3. Investimenti ricorrenti
Negli esempi precedenti, abbiamo effettuato semplici depositi una tantum, quindi ci siamo affidati interamente all'interesse composto per fornire rendimenti. Ma nella maggior parte dei sistemi di investimento e risparmio, effettuiamo depositi periodici per aumentare il nostro capitale.
Non esiste una funzione in forma chiusa per questo, quindi dobbiamo usare una funzione ricorsiva. Se assumiamo che il deposito venga effettuato all'inizio dell'anno, in modo che gli interessi vengano applicati al deposito, otteniamo quanto segue:
Quantità questo periodo = ( Importo l'ultimo periodo + deposito )×( 1 + tasso di interesse )
Dobbiamo ricalcolare per ogni periodo, come Quantità l'ultimo periodo cambia per ogni periodo. Quando effettui depositi, non solo aumenti il capitale di base (l'importo del puro investimento), ma aumenti anche l'importo che guadagna interessi.
Ecco perché iniziare presto è importante. Se depositi £ 500 all'inizio di ogni anno e inizi nell'anno 10, perderai un pagamento di interessi per il deposito dell'anno 9, due anni di interessi per il deposito dell'anno 8 e così via. Il tuo deposito iniziale aumenterebbe di £ 5.000, ma guadagneresti anche interessi di circa £ 1.300 solo sui depositi nell'arco di 10 anni.
Questo grafico mostra il valore finale di un 5%, investimento di 40 anni con un deposito iniziale di £ 1.500 e importi variabili di depositi annuali.
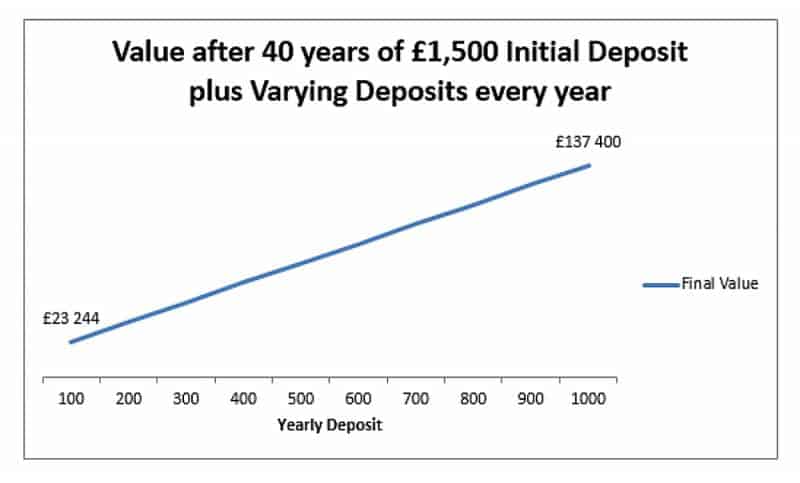
Possiamo vedere che i cambiamenti nel deposito annuale sono meno importanti dei cambiamenti nell'interesse o nel tempo, poiché abbiamo una relazione lineare anziché esponenziale. Ma in numeri assoluti, il deposito è ancora importante. £ 140.000 è molto maggiore di £ 20.000. Depositando £ 100 40 volte, finiamo con un investimento extra di £ 4000, quindi abbiamo circa £ 17.500 di interessi guadagnati. Con £ 1000 depositati ogni anno, noi depositare un extra di £ 40.000, ma il nostro interesse totale guadagnato è molto più alto a £ 96.000.
Guadagnavamo più interessi sui maggiori interessi prodotti dai maggiori depositi. L'asporto? Più interesse genera più interesse (e questo è il motivo del detto “i ricchi diventano più ricchi”).
E se non reinvestissimo i nostri dividendi o interessi?
Forse vogliamo semplicemente accumulare i nostri pagamenti di interessi, ma non li reinvestiamo. Se lo facciamo, non guadagneremo interessi su di loro. Ciò significa che abbiamo un interesse non composto. Come si confronta?
Questo grafico mostra un investimento iniziale di £ 1.500 senza altri depositi (quindi ignoriamo completamente i pagamenti ricorrenti). Abbiamo due variabili: una è il tasso di interesse (5% vs 6%) e l'altra è composta o meno (CIE = interesse composto guadagnato, NCIE = interesse non composto guadagnato).
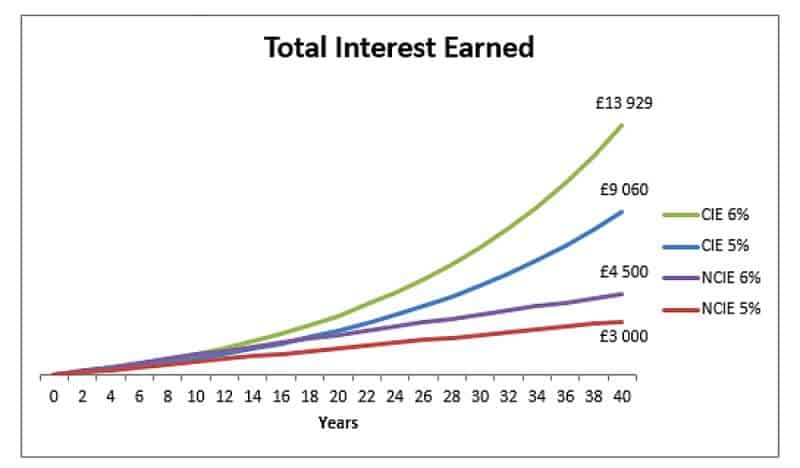
Le linee NCIE sono lineari perché moltiplichiamo semplicemente il numero di periodi per l'interesse che generiamo ogni anno. Guadagniamo £ 75 di interessi sul deposito di £ 1.500 (per 5%) e questo non cambia mai. Lo accumuliamo lentamente, £ 75 alla volta. Ma con la capitalizzazione, possiamo vedere che il primo anno è di £ 75, ma l'anno successivo guadagniamo £ 78,75 [(1500+75) × 1,05 – 1575], un extra di £ 3,75, che a sua volta contribuisce all'accumulo di interessi futuri. Questo continua a crescere nel tempo.
Ecco lo stesso grafico con capitalizzazione per 5% e 6% ma con depositi annuali di £ 300:
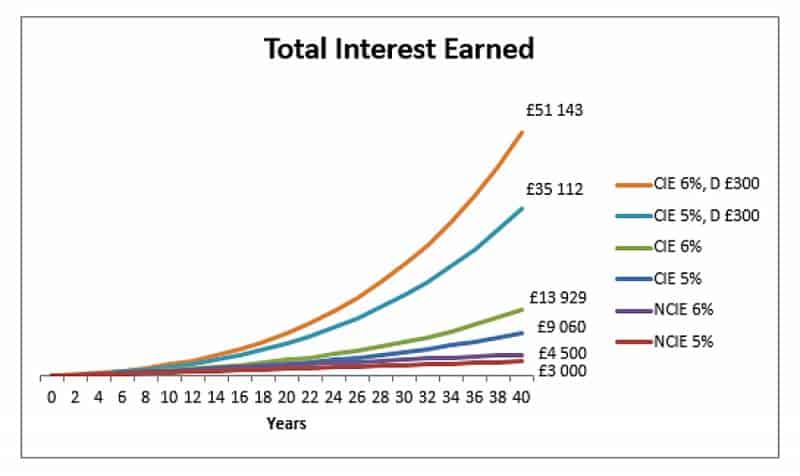
E un ultimo grafico, che mostra cosa accadrebbe se avviassimo uno schema di investimento con depositi di £ 250 a 5%, ma lo iniziassimo 10 anni dopo.
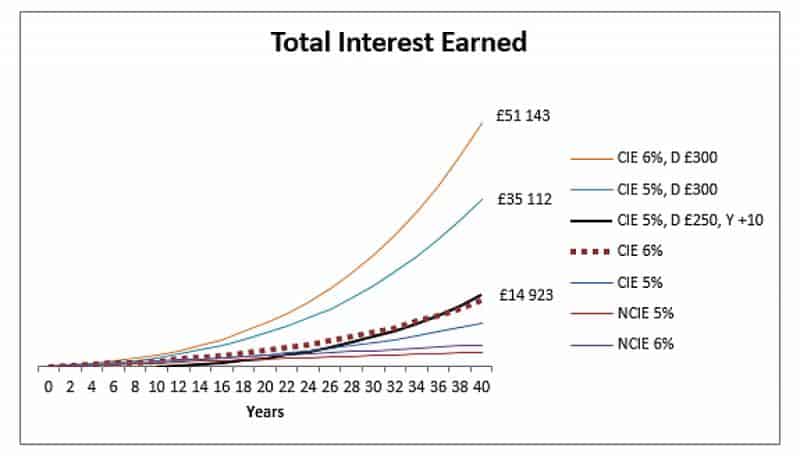
La cosa più importante da notare qui è che, poiché l'investimento viene avviato 10 anni dopo e il tasso di interesse è inferiore, l'investitore deve depositare £ 250 ogni anno solo per eguagliare la 6%, linea senza deposito. Nel periodo di 30 anni, si tratta di £ 7.500 extra di tasca propria solo a causa di un inizio ritardato e di un tasso di interesse inferiore di 1%.
Inoltre, dovremmo anche considerare che 40 anni di depositi di £ 300 aggiungeranno £ 12.000 in capitale, oltre all'investimento originale e agli interessi guadagnati.
Riepilogo
Le due componenti principali dell'interesse composto (tempo e tasso di interesse) insieme ai depositi ricorrenti possono fare un'enorme differenza nella crescita del tuo investimento nel tempo. Il rendimento delle azioni tra il 2004 e il 2017 è stato di 7,7% (Fonte: Schroders). Ciò significa una divergenza ancora più drammatica tra piani non composti e piani composti. E come possiamo vedere, se stai lasciando i soldi per il pensionamento tardivo, i tuoi figli o anche i tuoi nipoti, l'interesse composto diventa solo più potente con il tempo.
Un punto importante da notare è che il tuo interesse composto dovrebbe essere superiore all'inflazione. Mantenere le attività in conti a rendimento molto basso non coprirà l'inflazione, il che significa che la quantità di denaro grezza crescerà ma il suo potere d'acquisto rimarrà stagnante (o, nel peggiore dei casi, addirittura diminuirà).
A CityFALCON, aiutiamo i neofiti della finanza a diventare esperti e indipendenti nel prendere le loro decisioni finanziarie. Se sei interessato ai mercati azionari, puoi provare la nostra procedura guidata per iniziare qui.




23/07/2018 alle 19:52
abbastanza informativo e ben spiegato
27/07/2018 alle 9:03
Bel post sul blog!