Этот пост вдохновлен презентацией Кошик панджаби в Лондонский клуб ценностных инвестиций. Однако содержание сообщения - это точка зрения автора.
Мы всегда слышим, что надо начинать откладывать на пенсию рано. Мы должны реинвестировать наши дивиденды и найдите продукты, которые предлагают рецептуры. Немного более высокая процентная ставка может привести к гораздо более высокой конечной стоимости. Насколько это правда? Насколько сильны сложные проценты? Это зависит от трех факторов: 1) времени, 2) процентной ставки и 3) повторяющихся инвестиций.
Три фактора
1 раз
Первый фактор - время. Простая формула сложных процентов без дополнительных вложений:
Количество т = P (1 + р⁄п )нт
где
- P - основная сумма (первоначальные инвестиции),
- r - годовая номинальная процентная ставка,
- n - количество начисленных процентов за год,
- т - количество периодов начисления сложных процентов.
В своей основной форме это степенная функция y = c Икс (некоторое постоянное число, возведенное в степень с переменной степенью и принципалом «1»). Если мы посмотрим на этот график фундаментальной степенной функции, мы увидим изменение y с увеличением x. Если вы воспользуетесь формулой у = с Икс где c равно 3, а x продолжает увеличиваться от 1 до 5, вы можете видеть, что y увеличивается с 3 до 243.
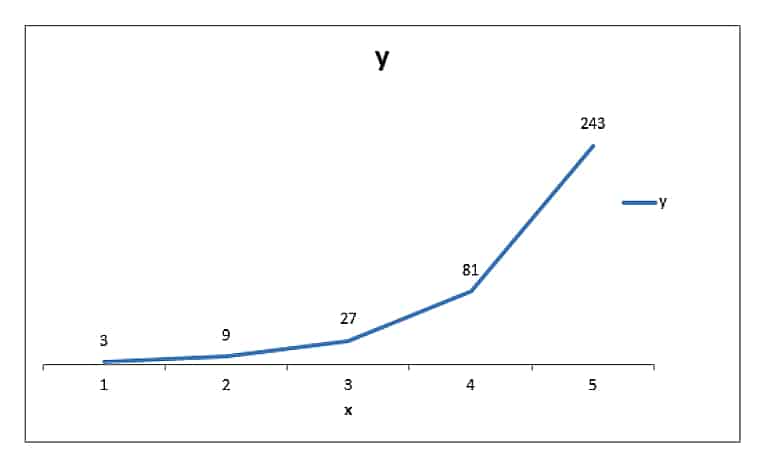
В финансах у нас есть гораздо меньшие константы, чем три (три будут доходностью 300% за период), но идея верна. Чем дольше применяется процентная ставка к инвестиции, тем более «сильным» становится процент. Также следует отметить, что вывод для диаграммы применяется к принципу 1 (USD, GBP, EUR, что угодно). У нас гораздо более крупные принципы и более длительные сроки в финансах.
Более реалистичный пример из финансов:
На диаграмме ниже представлена разовая инвестиция в размере 1500 фунтов стерлингов с постоянной процентной ставкой 5%. Первый начал инвестировать в начале года 0, а второй - в начале года 10 (то есть 10 лет спустя). По времени выхода на пенсию (40 лет сложения для года 0, 30 лет сложения для 10 года) более ранние инвестиции стоят на 63% больше.
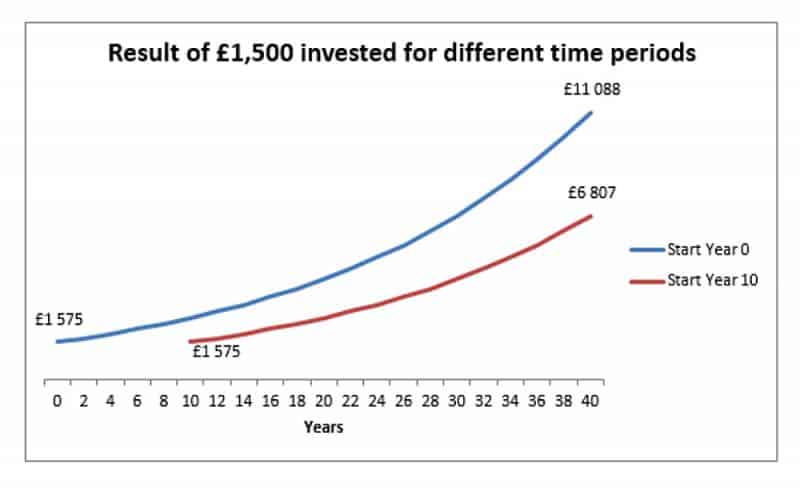
2. Процентная ставка
Второй важный фактор - это процентная ставка. По мере роста процентной ставки растет и доходность. В завышенных числах мы видим, что 33 (27) намного больше 23 (8) по сравнению с исходными базовыми значениями два и три.
Эта разница в ставках (3-2 = 1 = 100%) редко встречается в финансах, но принцип действует в меньших масштабах. На коротких шкалах (таких как три периода в нашем примере) разница обычно небольшая. Но в более длительных временных масштабах, таких как 40 периодов (сорок лет инвестиций), мы можем увидеть различия: (1 + 5%)40 = 700%, а (1 + 8%)40 = 2100%.
На приведенной ниже диаграмме показана процентная доходность простой инвестиционной стоимости одноразового депозита на основе сложного капитала за сорок лет. Единственная переменная - это процентная ставка. Как мы видим, доходность растет экспоненциально, точно так же, как временная составляющая влияет на доходность. По прошествии сорока лет 3% возвращает нам 325%, тогда как курс 10% дает нам 4500%. Для первоначального депозита в 1500 фунтов стерлингов это 4875 фунтов стерлингов против 67 500 фунтов стерлингов.
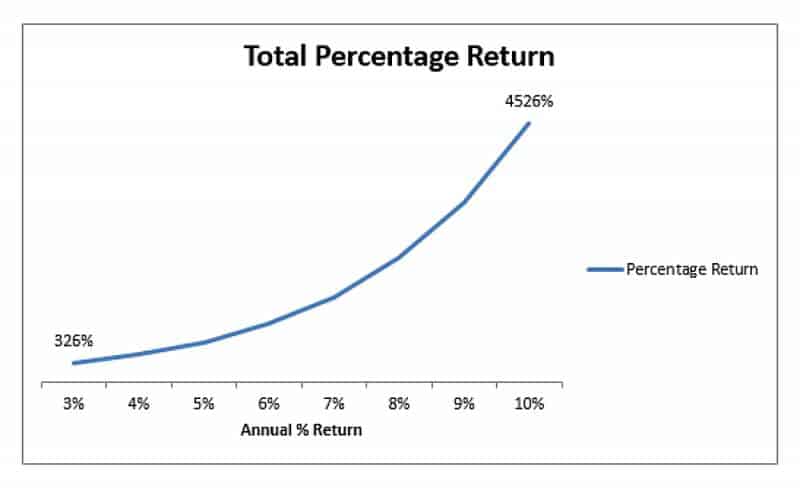
3. Периодические инвестиции
В приведенных выше примерах мы делали простые одноразовые вклады, а затем полностью полагались на сложные проценты для получения прибыли. Но в большинстве инвестиционных и сберегательных схем мы делаем периодические вклады, чтобы увеличить нашу основную сумму.
Для этого нет функции замкнутой формы, поэтому мы должны использовать рекурсивную функцию. Если предположить, что депозит был сделан в начале года, так что проценты начисляются на депозит, мы получим следующее:
Количество этот период = (Сумма Последний период + депозит) × (1 + процентная ставка)
Мы должны пересчитывать за каждый период, так как Количество Последний период меняется за каждый период. Делая депозиты, вы не только увеличиваете базовую сумму (чистую сумму инвестиций), но также увеличиваете сумму, на которую начисляются проценты.
Вот почему так важно начинать раньше. Если вы вносите 500 фунтов стерлингов в начале каждого года и начинаете с 10-го года, вы пропустите одну выплату процентов по депозиту 9-го года, два года процентов по депозиту 8-го года и так далее. Ваш первоначальный депозит вырастет на 5000 фунтов стерлингов, но вы также будете получать проценты в размере около 1300 фунтов стерлингов только по вкладам в течение 10 лет.
На этой диаграмме показана окончательная стоимость 40-летней инвестиции 5% с начальным депозитом в 1500 фунтов стерлингов и различными суммами годовых депозитов.
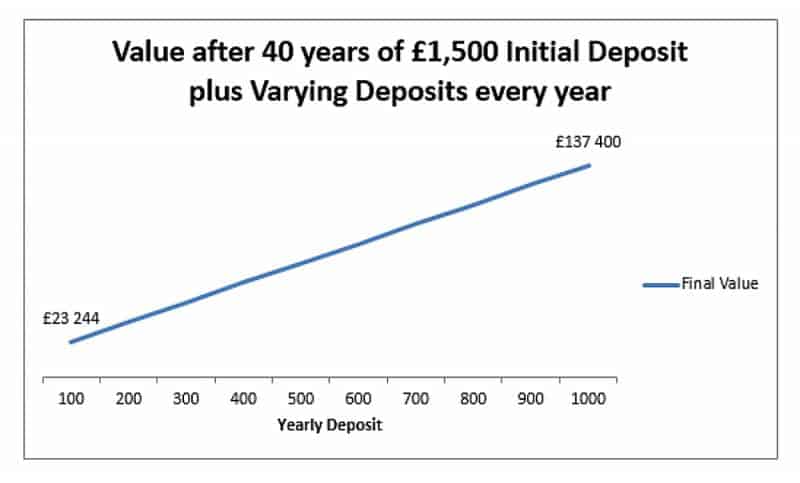
Мы видим, что изменения годового депозита менее важны, чем изменения процентов или времени, поскольку у нас линейная зависимость, а не экспоненциальная. Но в абсолютных цифрах залог все равно важен. 140 000 фунтов стерлингов намного больше, чем 20 000 фунтов стерлингов. Внося 100 фунтов стерлингов 40 раз, мы получаем дополнительно 4000 фунтов стерлингов вложения, таким образом, мы получаем около 17 500 фунтов стерлингов в виде процентов. Ежегодно вкладывая 1000 фунтов стерлингов, мы депозит дополнительные 40 000 фунтов стерлингов, но наши общие проценты намного выше и составляют 96 000 фунтов стерлингов.
Мы получали больше процентов от более высоких процентов по депозитам. Вывод? Больше интереса - значит больше интереса (отсюда и говорят «богатые становятся богаче»).
Что, если мы не реинвестируем наши дивиденды или проценты?
Возможно, мы хотим просто накапливать процентные платежи, но не реинвестируем их. Если мы это сделаем, мы не будем получать на них проценты. Это означает, что у нас есть проценты без начисления процентов. Как это сравнить?
На этой диаграмме показаны первоначальные инвестиции в размере 1500 фунтов стерлингов без каких-либо других вкладов (поэтому мы полностью игнорируем повторяющиеся платежи). У нас есть две переменные: одна - это процентная ставка (5% против 6%), а другая - начисление сложных процентов (CIE = начисленные проценты с начислением сложных процентов, NCIE = заработанные проценты без начисления сложных процентов).
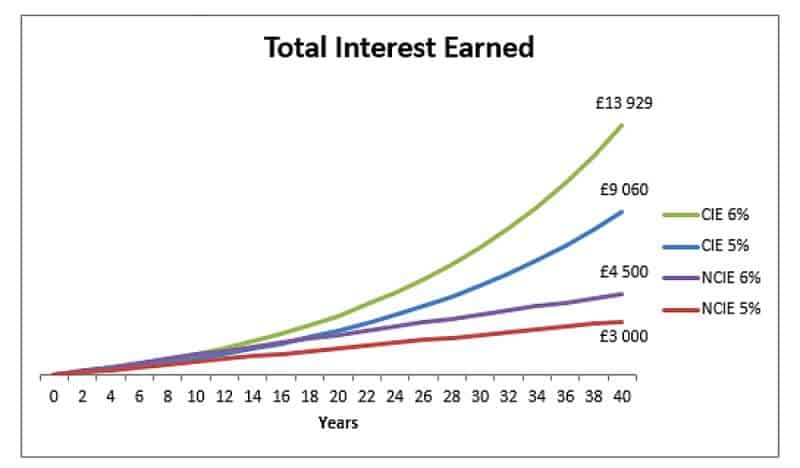
Линии NCIE линейны, потому что мы просто умножаем количество периодов на процент, который мы генерируем каждый год. Мы вносим 75 фунтов стерлингов на депозит в размере 1500 фунтов стерлингов (для 5%), и это никогда не меняется. Мы просто медленно накапливаем его, 75 фунтов стерлингов за раз. Но при сложном начислении мы видим, что первый год составляет 75 фунтов стерлингов, но в следующем году мы получаем 78,75 фунтов стерлингов [(1500 + 75) × 1,05 - 1575], то есть дополнительно 3,75 фунтов стерлингов, что само по себе способствует накоплению процентов в будущем. Это продолжает расти с течением времени.
Вот тот же график с начислением сложных процентов для 5% и 6%, но с годовым депозитом в 300 фунтов стерлингов:
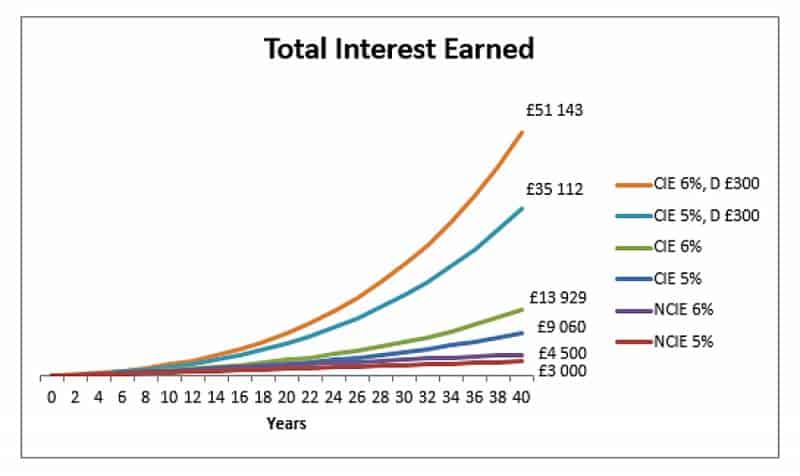
И последний график, показывающий, что произошло бы, если бы мы начали инвестиционную схему с депозитами в 250 фунтов стерлингов на 5%, но мы начали ее 10 лет спустя.
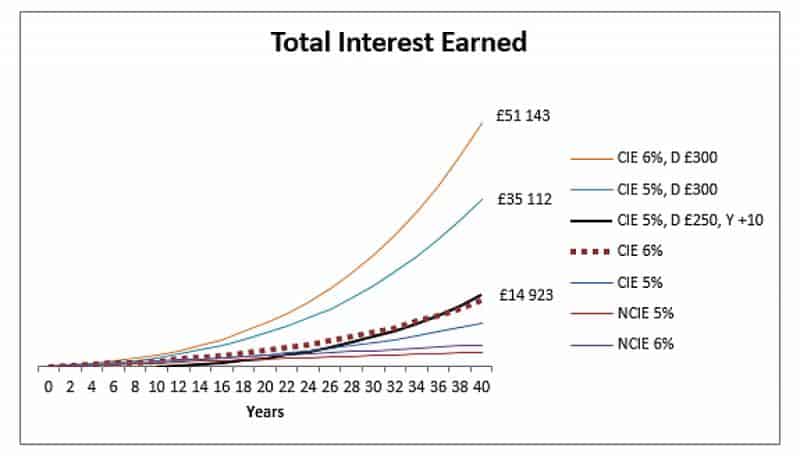
Здесь важно отметить, что, поскольку инвестиции начинаются на 10 лет позже, а процентная ставка ниже, инвестор должен ежегодно вносить 250 фунтов стерлингов только для соответствия бездепозитной линии 6%. За 30-летний период это дополнительные 7500 фунтов стерлингов из собственного кармана только из-за позднего начала и процентной ставки, которая на 1% ниже.
Более того, мы также должны учитывать, что 40 лет вкладов в размере 300 фунтов стерлингов добавят 12000 фунтов стерлингов в основной капитал сверх первоначальных инвестиций и заработанных процентов.
Резюме
Два основных компонента начисления сложных процентов (время и процентная ставка) в сочетании с повторяющимися депозитами могут иметь огромное значение в том, насколько ваши инвестиции будут расти с течением времени. Доходность акций с 2004 по 2017 год составила 7,7% (Источник: Schroders). Это означает еще более резкое расхождение между планами без начисления сложных процентов и планами с начислением сложных процентов. И, как мы видим, если вы оставляете деньги на поздний выход на пенсию, своим детям или даже своим внукам, сложный процент со временем только усиливается.
Следует отметить один важный момент: ваши сложные проценты должны быть выше инфляции. Хранение активов на счетах с очень низкой процентной доходностью не покроет инфляцию, что означает, что чистая сумма денег будет расти, но их покупательная способность останется на прежнем уровне (или, в худшем случае, даже снизится).
В CityFALCON мы помогаем новичкам в сфере финансов стать сообразительными и независимыми в принятии финансовых решений. Если вас интересуют фондовые рынки, вы можете попробовать наш мастер по началу работы здесь.




23.07.2018 в 7:52 пп
довольно информативный и хорошо объясненный
27.07.2018 в 9:03 дп
Хороший пост в блоге!